人教版高中数学必修四知识点归纳总结，期末复习必备！

高中数学必修四知识点总结

2、角

的顶点与原点重合，角的始边与

轴的非负半轴重合，终边落在第几象限，则称

为第几象限角．第一象限角的集合为

第二象限角的集合为

第三象限角的集合为

第四象限角的集合为

终边在

轴上的角的集合为

终边在

轴上的角的集合为

终边在坐标轴上的角的集合为

3、与角终边相同的角的集合为

4、已知是第几象限角，确定

所在象限的方法：先把各象限均分

等份，再从轴的正半轴的上方起，依次将各区域标上一、二、三、四，则原来是第几象限对应的标号即为

终边所落在的区域．

5、长度等于半径长的弧所对的圆心角叫做

弧度的角．

6、半径为

的圆的圆心角所对弧的长为

，则角的弧度数的绝对值是

．

7、弧度制与角度制的换算公式：

，

，

．

8、若扇形的圆心角为

，半径为

，弧长为

，周长为

，面积为

，

则

，

，

．

9、（一）设是一个任意角,它的终边与单位圆交于点

,那么:(1)

叫做的正弦,记做

,即

；（2）叫做的余弦,记做

,即

；（3）

叫做的正切,记做

,即

。

（二）设是一个任意大小的角，的终边上任意一点

的坐标是

，它与原点的距离是

，则

，

，

．

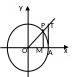
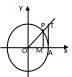
10、三角函数在各象限的符号：第一象限全为正，第二象限正弦为正，第三象限正切为正，第四象限余弦为正．

11、三角函数线：

，

，

．

12、同角三角函数的基本关系式：

；

．

13、三角函数的诱导公式：

，

，

．

，

，

．

，

，

．

，

，

．

口诀：函数名称不变，符号看象限．

，

．

，

．

口诀：函数名改变，符号看象限．

14、图像变换的两种方式：

（一）函数

的图象上所有点向左（右）平移

个单位长度，得到函数

的图象（

>0是左移；

<0是右移）；再将函数

的图象上所有点的横坐标伸长（缩短）到原来的

倍（纵坐标不变），得到函数

的图象；再将函数

的图象上所有点的纵坐标伸长（缩短）到原来的

倍（横坐标不变），得到函数

的图象

．

（二）函数

的图象上所有点的横坐标伸长（缩短）到原来的

倍（纵坐标不变），得到函数

的图象；再将函数

的图象上所有点向左（右）平移

个单位长度（>0是左移；<0是右移）；得到函数的图象；再将函数的图象上所有点的纵坐标伸长（缩短）到原来的

倍（横坐标不变），得到函数

的图象

．

函数

的性质：

①振幅；②周期：

；③频率：

；④相位：

；⑤初相：．

函数

，当

时，取得最小值为

；当

时，取得最大值为

，则

，

，

．

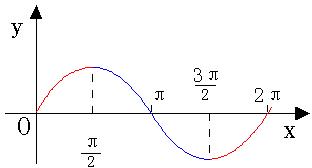
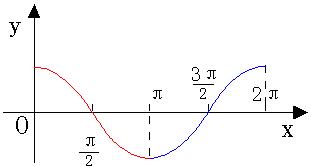
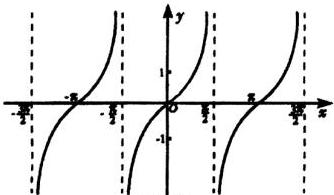
15 、正弦函数、余弦函数和正切函数的图象与性质：

图象
定义域
值域
最值	当 时， ；当 时， ．	当 时， ；当 时， ．	既无最大值也无最小值
周期
奇偶性	奇函数	偶函数	奇函数
单调性	在 上是增函数；在 上是减函数．	在 上是增函数；在 上是减函数．	在 上是增函数．
对称性	对称中心 对称轴	对称中心 对称轴	对称中心 无对称轴

16.三角函数奇偶性规律总结（

）

函数

为奇函数的条件为

函数

为偶函数的条件为

函数

为奇函数的条件为

.

函数为偶函数的条件为

函数为奇函数的条件为

它不可能是偶函数．

17．向量：既有大小，又有方向的量． 数量：只有大小，没有方向的量．

有向线段的三要素：起点、方向、长度． 零向量：长度为

的向量．

单位向量：长度等于

个单位的向量． 平行向量（共线向量）：方向相同或相反的 非零向量．

规定：零向量与任一向量平行．

相等向量：长度相等且方向相同的向量． 相反向量：长度相等且方向相反的向量．

1

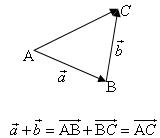
8 、向量加法：⑴三角形法则的特点：首尾相连．⑵平行四边形法则的特点：共起点．

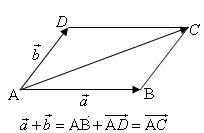
⑶三角形不等式：

．

⑷运算性质：①交换律：

；

②结合律：

； ③

．

⑸坐标运算：设

，

，则

．

19、向量减法运算：

⑴三角形法则的特点：共起点，连终点，方向减向量的终点指向被减向量终点．（见上图）

⑵坐标运算：设

，

，则

．

设、

两点的坐标分别为

，

，则

．

20、向量数乘运算：

⑴实数

与向量

的积是一个向量，这种运算叫做向量的数乘，记作

．

①

；②当

时，

的方向与

的方向相同；当

时，的方向与的方向相反；当

时，

．0=

⑵运算律： ①

； ②

； ③

． ⑶坐标运算：设

，则

．

(4)

21向量共线条件：(1)向量

与

共线，当且仅当有唯一一个实数

，使

．

(

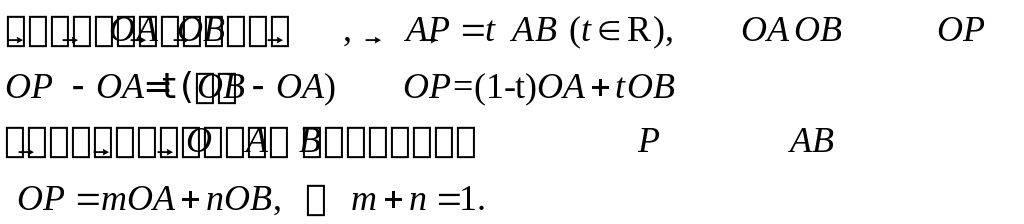
2) 共线的坐标表示，设，，其中

，则当且仅当

时，向量、

共线．

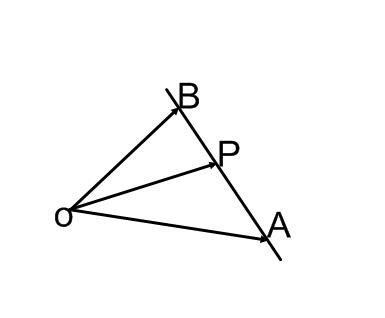
22、平面向量基本定理：如果

、

是同一平面内的两个不共线向量，那么对于这一平面内的任意向量，有且只有一对实数

、

，使

．（不共线的向量

、

叫做这一平面内所有向量的一组基底）

小结论：（1）若、是同一平面内的两个不共线向量，

（2）若、是同一平面内的两个不共线向量，

23、分点坐标公式：设点

是线段

上的一点，

、

的坐标分别是

，

，当

时，可推出点的坐标是

．（会写出向量坐标，会运算。）

24、平面向量的数量积：

⑴定义：

．零向量与任一向量的数量积为

．

：在

方向上的投影

：在方向上的投影

注意：务必要算对两个非零向量的夹角：设两个非零向量

与

, 称

为向量 与 的夹角

， 注意在两向量的夹角定义，两向量必须是同起点的。

⑵性质：设和都是非零向量，则①

．

②当与同向时，

；当与反向时，

；

或

． ③

．

⑶运算律：①

；②

；③

．

⑷坐标运算：设两个非零向量，，则

．

（5）若

，则

，或

．

（6）设，，则

．

（7）设、都是非零向量，，，

是与的夹角，

则

．

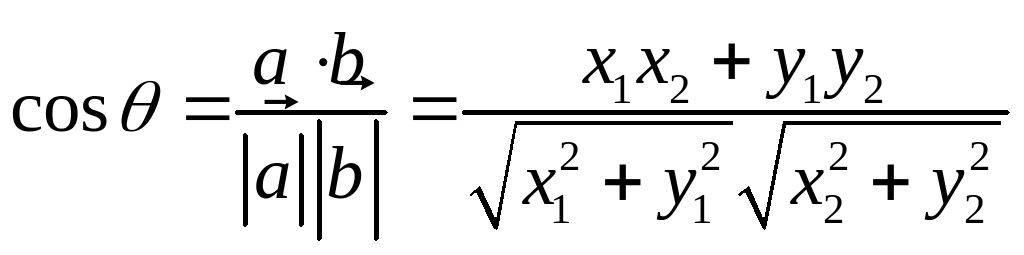
25、两角和与差的正弦、余弦和正切公式：

⑴

；⑵

；

⑶

；⑷

；

⑸

变形：（

）；

⑹

变形：（

）．

26、二倍角的正弦、余弦和正切公式：

⑴

． 变形：

⑵

变形得到降幂公式：

，

．

⑶

．

27、

，其中

．

[2010高考题解析，规范解题步骤]已知函数

，其图象过点（

,

）．（Ⅰ）求 的值；（Ⅱ）将函数

的图象上各点的横坐标缩短到原来的

，纵坐标不变，得到函数

的图象，求函数

在 [0,

] 上的最大值和最小值．

解：（Ⅰ）因为

所以

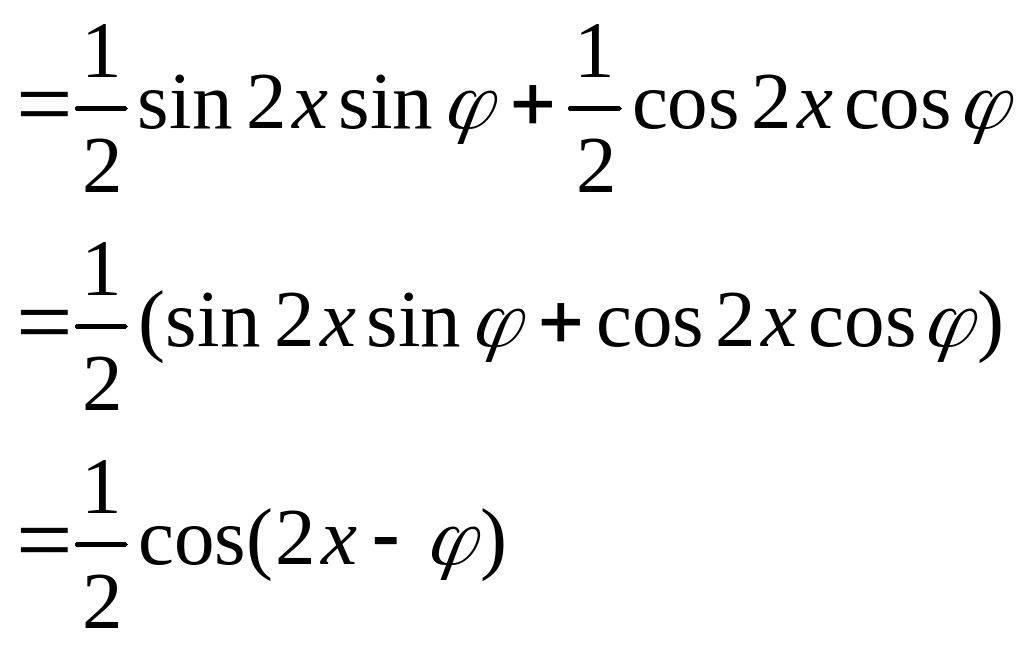
又 函数图像过点

所以

即

又

所以

（Ⅱ） 由（Ⅰ）知

，将函数

的图像上各点的横坐标缩短到原来的 ，纵坐标不变，得到函数

的图像，可知

因为

所以

因此

故

所以

在

上的最大值和最小值分别为 和